We have compiled a zip-file with a bunch of old exams, as well as their solutions. The newer ones, 2011 and 2012, are most relevant.
Good luck!

We have compiled a zip-file with a bunch of old exams, as well as their solutions. The newer ones, 2011 and 2012, are most relevant.
Good luck!
Since the lectures and the weekly exercises are not completely in sync, we are adding a couple of exercises which we recommend you to go through before the midterm exam.
If you feel that you need more training in vector analysis, consider doing these exercises that we have borrowed from D. J. Griffiths’ book “Introduction to Electrodynamics”. If you feel that you have mastered the weekly exercises this far without getting stuck on the vector calculations, feel free to skip this problem set.
Most of these problems come without solutions, but you can test your understanding at the group sessions.
We have made a small demo that will allow you to play around with electric field lines in your web browser. You can place and move around charged particles to see how the field changes as you make your own charge configuration.
Note that there are some limitations to this simulation, leaving it a bit unphysical when it comes to lines that might end up in open space, wrong field line density and other quirks. All in all it should be correct to a decent approximation, though.
For the programming enthusiasts out there, the simulation is created using Javascript and HTML5. You can check out the source code here.
Enjoy!
Ok, so we’re working on the home exam in classical mechanics and I decided to spend some time simulating the solution of the first exercise. Probably not the wisest way to spend time during an home exam, but what the heck. I’m learning some Javascript and HTML5, plus the fact that it’s always fun to verify results by looking at something moving!
So here you go. A pendulum on a cart.
I won’t go into details about deriving and solving the Lagrange equation for this system now, but I might get back to that at a later time. And of course there will be some added controls to this so you could set the initial positions, velocities and stuff. Sometime later, I hope.
In electrostatics we found it very convenient to introduce the concept of the electric potential. It gave us a straight forward way of calculating electric fields without doing any vector calculations or using any symmetry arguments. Can we introduce something similar for magnetic fields? It turns out that because magnetic fields are divergence less we can find a vector potential who’s curl gives us the magnetic field! Even though this magnetic vector potential is not as useful as the electrostatic potential in elementary applications, it turns out to be of major importance in electrodynamics as well as classical mechanics and quantum mechanics. It might therefore be a good idea to get familiar with the concept and some of it’s properties already, especially if you are taking a degree in physics. In this note I explain how to find the vector potential, the concept of a gauge transformation and it’s fundamental equations relating it to currents in both electrostatics and electrodynamics. Read more here:
* Image found at http://en.wikipedia.org/wiki/File:VFPt_dipole_magnetic3.svg / CC BY-SA 3.0
I guess you are pretty exhausted after the midterm exam this week and a lot of you have probably had other exams to deal with as well. What better time to share a game with you to put your minds at ease for a little while.
The game is called Nanoparticles and was written by me about half a year ago. It is based on Coulomb’s law with a few modifications and Newtonian physics. But instead of having you calculate anything, the game does it all for you in the background. You can download the game for Ubuntu, Linux, Windows and Nokia phones here (Mac and Android versions will be available sometime in the future):
Your mission is to make sure the positive particles you control does not crash into the negative ones. That would cause it to annihilate. To do this, you need to place out other positive and negative particles to keep your particle away for as long as possible.
The game is also open source, so if you’re interested in programming and C++, you can have a look at the source code too. More information about the game and how to obtain the source code is found here.
The dipole moment of a configuration of charges is an important concept in electromagnetism, but in most introductory texts it might seem like the dipole moment is only defined for two opposite point charges separated by a distance. This is however not the case. The dipole moment can be defined for any configuration of charges where the net charge is zero.
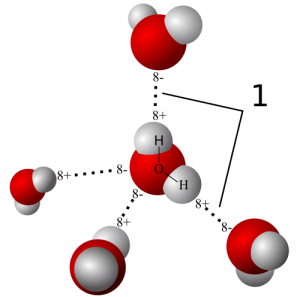
H20 is a polar molecule which means that it has dipole moment. However the H20 molecule is not just two point charges separated by a distance. So how do we then define its dipole moment? Source: Qwerter/Wikipedia
The dipole moment is also crucial in order to undersant how molecules and atoms are affected when they are placed in electric fields as well as understanding the phenomenon of “polarization” of matter.
If you want to learn more about why dipole moments are important and about its generality the following note might be of interest to you:
matplotlib is an amazing framework to do visual plots in Python. It compares well with GnuPlot and beats Matlab’s plotting abilities by having more features. Although it does lack some 3D support, you may simply choose a different framework for 3D plots thanks to Python’s flexibility . In which case I would recommend Mayavi as a superb 3D plotting engine which I have written about before.
But now, let’s have a look at matplotlib’s animation capabilities. The script below shows a very easy approach to animation in matplotlib. This results in an animation of the standing wave shown here:
The script is as follows:
Continue reading
It’s been a while since we’ve posted anything here. Sorry about that. It has just been too much to do lately to find the time to write new posts.
This post is also arriving a bit late to be useful for anyone this semester, but what it shows might be useful for others. Or maybe for someone taking the FYS1120 course at a later time. So I’ll post it here still.
In mandatory exercise 2 we needed to load a huge file containing data from an AM radio signal. This was available a Matlab file and as a text file with all the values on each row. Those of us using Python realized quite quickly that most of the time spent on this exercise went to load the data before performing any computations on the data.
However, in proper hindsight, I thought it might have been a better idea to save the file as binary data instead of as a text file. After all, binary data saves space and usually is a bit quicker to load.
Doing this in NumPy is extremely simple. Just load the text file data and save it back in NumPy’s binary format: