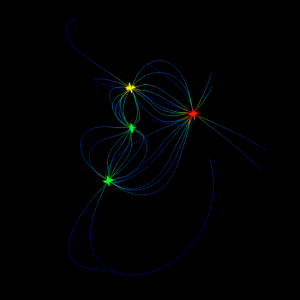
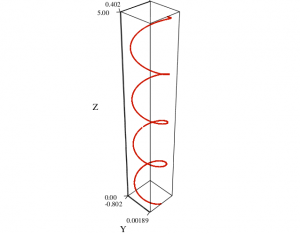
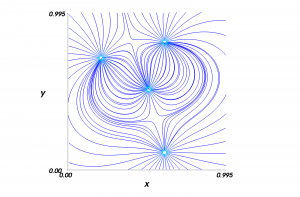
In one of my earlier posts about Mayavi, I wrote about how you could visualize 2D field line plots using the flow function. At the end of that post I added that Mayavi is actually best at 3D plotting, and to follow up on that I’ll show you some of these plots with a few example Python scripts you might try out on your own.
First of all, you might want to know how to install Mayavi. For those lucky ones of you who have freed yourself and jumped on the Linux bandwagon, installing Mayavi should be quite easy. If you are using Ubuntu in particular, you may just install the package mayavi2 using either Synaptic or apt-get. If you are on Windows or Mac, you may either install Enthought’s own Python distribution (EPD) or give a shot at compiling on your own. Just note that EPD is quite expensive, even though all its components are open source, but if you are a student or academic user you could go ahead and download the academic version for free. It is basically the same as the commercial one, but with an academic license. (Kudos to Enthought for both making Mayavi open source, building an business model around it and still providing a great solution for students!)
Now, Enter 3D!
The way you do your plots in Mayavi depends on what you want to express. Most likely, you would prefer to show some simple plots giving just the necessary amount of information to tell you how the electric field behaves around your charges. A simple example of this is shown below: