Carl Friedrich Gauss (1777 – 1855) by G. Biermann (1824-1908)
Earlier today, enjoying a warm cup of coffee with a friend of mine,we got into a discussion about some math and ended up contemplating on how to prove the sum formula for the n first natural numbers.
The proof is rumored to first have been done by Gauss when he was only a child.
Let 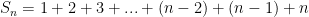
just rewriting the terms backwards we get
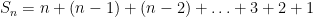
now adding these two expressions for the sum we obtain
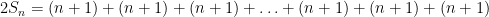
and since we had n terms in the original sum we now have 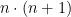 ‘s, so
‘s, so
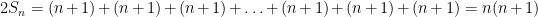
so..
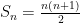
Neat. On a computer this would severely reduce the number of operations that would have to be done to compute such a sum. Imagine having to sum up the first million natural numbers and let’s suppose the computer requires one operation for adding, multiplying, dividing and so forth. Then implementing this formula would reduce the numbers of operations from 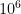 to 3.
to 3.
is expressed just in x? Probably not, but it might actually sometimes be useful to know. The expression might for example turn up when you’ve done a trigonometric substitution in an integral. So I decided how to go about to show the trigonometric identities
,
,
.