This post is from an earlier year, meaning the information here is likely outdated. You should look for a newer post from the current year to get the newest exercises and notes.
The oblig has been posted on the course pages.
You can find it here under “Obligatoriske oppgaver”.
Please note that last weeks exercises included an oblig warm-up. This can be useful if you want to test yourself with a simpler problem before going ahead with the whole oblig.
In addition, you’ll find the note about Jacobi’s method on this page, under the link named “Numerical solutions of Laplace’s equation”.
You’ll find the due date in the oblig itself.
Good luck!

Skal oppgave e). og f). løses analytisk eller numerisk?
Ja. Du kan velge selv, eller velge både numerisk og analytisk løsning, som sannsynligvis er det du lærer mest av.
hei
hvor kan jeg finne den Jacobis metode til den oppgave c ??
Nederst på denne siden ligger det en lenke som heter “Numerical solutions of Laplace’s equation”:
http://mindseye.no/fys1120/notes/
Hi!
In part c of the oblig we are asked to use Jacobi’s method to find V(x,y) in the domain [0,a] X [0,b].
As i am reading this now, that is a line segment of length |a-b| on the y-axis. Is this correct or do you mean the domain [a,0] X [0,b]?
Hi Knut,![[0,a]\times[0,b] [0,a]\times[0,b]](http://s0.wp.com/latex.php?latex=%5B0%2Ca%5D%5Ctimes%5B0%2Cb%5D&bg=ffffff&fg=000&s=0) means the rectangle with corners
means the rectangle with corners  ,
,  ,
, 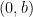 ,
, 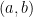 . That is to say, the square bracket before the multiplication denotes the limits in
. That is to say, the square bracket before the multiplication denotes the limits in  and the square bracket after the multiplication holds the limits in
and the square bracket after the multiplication holds the limits in 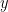 . This notation is quite common, so you are likely to see it again.
. This notation is quite common, so you are likely to see it again.
the notation
In fact, the domain![[a,0]\times[0,b] [a,0]\times[0,b]](http://s0.wp.com/latex.php?latex=%5Ba%2C0%5D%5Ctimes%5B0%2Cb%5D&bg=ffffff&fg=000&s=0) would be the same rectangle, although written in a non-standard way.
would be the same rectangle, although written in a non-standard way.