This post is from an earlier year, meaning the information here is likely outdated. You should look for a newer post from the current year to get the newest exercises and notes.
This week the problems focuses mainly on circuits and Kirchhoff’s laws.
1)
a) .
Indicating that current nr.2 and 3 is directed in the opposite way of what was assumed.
b)
.
c) Of course the second voltage supply is also doing work on the charges in the current, so this is the reason that In this case it is actually doing negative work.
2)
a) At , the moment when the switch is closed, there is no charge on the capacitor and therefore no potential difference over it. This means that the current at this time will be as if there were no capacitor in the circuit, so
As time goes to infinity, the capacitor gets charged up. At some point it will reach a potential difference equal to the potential difference of the voltage supply and the current will be zero.
b) At it is a ressistance R in one subcircuit, while there is no ressistance in the other, so the current will go trough the circuit with no ressistance. Since there is no resistance
, which means that the capacitor gets charged up infinitely fast.
When the capacitor is fully charged, no current will go towards it and therefore all current will go trough the resistance. This means that we now have
3)
a)
b)
c)
4)
a) Here I used Kirchhoff’s laws to get 5 equations which I put in a matrix, did rowreduction and got .
b) (correction: Filip Sund)

The answer both I and the “official” solution got to 4b) were ~1.812 ohm:
[latex]R = \frac{\varepsilon}{I} = \frac{\varepsilon}{I_1 + I_2} = \frac{\varepsilon}{I_4 + I_5}[/latex]
where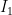 and
and 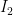 are the currents through the upper resistances,
are the currents through the upper resistances, 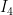 and
and 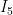 through the lower.
through the lower.
Thank you for that Filip! I’m sure that is the correct answer then 🙂 I’ll correct it.
Hey Andreas! 🙂 Ah, thank you. I must have overseen that we actually had an internal ressistance. I’ll fix that right up.
Hey!
Good lookin’ answers, dude. However, in 2), you need to account for an inner resistance r in the battery (this only gives you an added resistance r, as in a series circuit). The answers i got were then
2a) I_0 = eps/(R + r)
I_inf = 0
2b) I_0 = eps/r
I_inf = eps/(R + r)